Алгебра: 2^18 * 0.5^19 = ? Повний розв язок як це робити.

2^18 * 0.5^19 = ?
Повний розв'язок як це робити.

Ответы

amir45 15.10.2020 15:26

0.5

Объяснение:

$2^{18}*0.5^{19}=2^{18}*\left(\frac{1}{2} \rihgt)^{19}=2^{18}*(2^{-1})^{19}=2^{18}*2^{-19}=2^{-1}=\frac{1}{2}=0.5$

ПОКАЗАТЬ ОТВЕТЫ

Set1z1337 15.10.2020 15:26

$2^{18} *0,5^{19} \\2^{18} *2^{-19} \\2^{-1} \\\frac{1}{2}, 0,5$

Шаги решения:

1) Преобразование десятичной дроби в обыкновенную по формуле: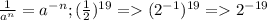 $\frac{1}{a^{n} } =a^{-n}; (\frac{1}{2} )^{19} = (2^{-1})^{19} = 2^{-19}$

2) Вычислить степени:

$2^{18}*2^{-19} = 2^{18-19} = 2^{-1}$

3) Используем свойства степеней: при возведении выражения в степень -1 получается обратное к исходному выражение: $\frac{1}{2}$

4) $\frac{1}{2}$ => 0,5

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

SERGUES 11.04.2020 13:46

Ksyufenka 11.04.2020 13:46

Как это решить и какой ответ получится?...

asya343434 11.04.2020 23:23

EeVoNGuY 13.04.2020 05:40

Самостоятельная работа В-1 Только Часть А...

Медина00 23.09.2019 08:40

бабелон 23.09.2019 08:40

Разность многочленов 8x2-xy-3y2 и -7x2+xy-3y2 равна:...

azat20142014 01.07.2019 22:30

Найти производную функцию y=|x²-14x+45|...

Eveliinaa 01.07.2019 22:30

Blarow 01.07.2019 22:30

KeyTii 01.07.2019 22:30

Разложите на множители 5a+5b+c(a+b) (a-4)²-3a(a-3)...