№1Решить систему матричным Решить систему по формулам Крамера
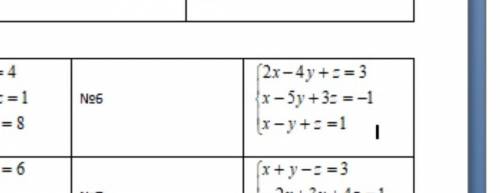
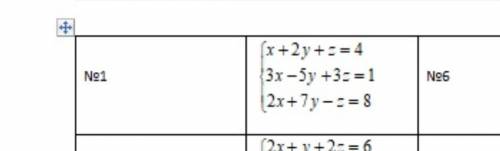
Другие вопросы по теме Алгебра
Популярные вопросы
- Терминология кормления ; епископ,ересь, пожилое,местничество...
2 - Які з наведених функцій завжди повертають результат дійсного типу?...
3 - открыть скобки. Буду очень благодарна.1. Michael said that I …………………………......
1 - Перевести с английского на русский (БЕЗ ПЕРЕВОДЧИКА) 1. to occupy;...
3 - с заданием еки куйши, онерлеринди бирдей салындар деген кыз созинин...
1 - Остались тут ещё добрые люди?Можете с сочинением-рассуждением?Только...
2 - Определите вид фигуры по представленной развертки. Развертка трекгольной...
3 - Вік головного героя твору івана сили...
2 - Внимательно прочитайте текст. Эта улыбка пленила меня и привела...
1 - СДЕЛАЙТЕ МНЕ как записать координаты точкиА(5;-7)...
1
Объяснение:
Вычислим определители матрицы:
ответ: x=2 y=0 z=-1.