№1представить выражение в виде многочлена стандартного вида: (a+3)^{2}+(a-3)(a+3)+6a №2разложить на множители: а)xy-2y б)16a^{2}-81 в)3x^{2}-6x^{3} г)x^{2}-10x+25 д)3(x-1)+y(x-1) е)2a^{2}-4ab+2b^{2} №3разложить на множители многочлен a^{2}-3ab+3a-9b и найти его числовое
значение при a=1,b=-\frac{1}{3}

№1 Многочлен стандартного вида - сумма одночленов стандартного вида. Одночлен стандартного вида имеет определенный порядок записи: на первом месте число, а затем идут переменные в алфавитном порядке. 

№2

а)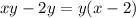

б)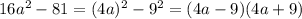  

в)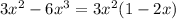  

г)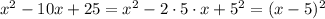

д)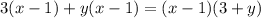  

е)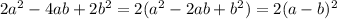  

№3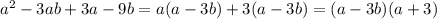  

При a=1; b=-1/3 Получим 8 

1)(a+3)^2+(a-3)(a+3)+6a=a^2+6a+9+a^2-9+6a=2a^2+12a

2)a)xy-2y=y(x-2)

b)16a^2-81=(4a-9)(4a+9)

в)3x^2-6x^3=3x^2(1-2x)

г)x^2-10x+25=(x-5)^2

д)3(x-1)+y(x-1)=(3+y)(x-1)

е)2a^2-4ab+2b^2=2(a^2-2ab+b^2)=2(a-b)^2

3)a^2-3ab+3a-9b=(a^2-3ab)+(3a-9b)=a(a-3b)+3(a-3b)=(a+3)(a-3b)=(1+3)(1+3/3)=4*2=8