1февраля был выдан полугодовой кредит на развитие бизнеса на следующих условиях: — в конце каждого месяца, начиная февраля, текущий долг увеличивается на p%; — первого числа следующего месяца должна быть произведена выплата, уменьшающая сумму долга на определенное число процентов от суммы взятого кредита; — первая выплата должна уменьшить сумму долга на 5% от суммы кредита, вторая — на 10%, третья — на 15%, четвертая — на 20%, пятая и шестая — на 25% каждая (таким образом, после шести выплат заёмщик возвратит банку сумму кредита вместе с ежемесячными процентами). после погашения всего кредита оказалось, что сумма выплат на 34% больше суммы взятого кредита. найдите значение p.
Другие вопросы по теме Алгебра
Популярные вопросы
- Используя текст параграфа и карты, сделайте краткие выводы: 1) о...
2 - Какие климаты наиболее характерны для территории России? Назовите...
3 - Сопоставьте карту плотности населения с картой климатических поясов....
1 - Вспомните из курса «Географии материков и океанов» основные типы...
3 - Подумайте, как влияет климат на набор наиболее популярных видов...
2 - Каким образом чередование Сибирского антициклона и Азиатского минимума...
2 - Проанализируйте климатические особенности своей области (республики,...
3 - Какие климатические области выделяют в пределах умеренного климатического...
2 - K бассейнам каких океанов относятся наиболее крупные реки России?...
3 - Посмотрите по климатической карте, где расположены такие крупные...
3
Возьмём сумму долга за 100 руб., чтобы численное значение долга совпадало с численным значением процентного остатка от него, и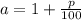 .
.
Как посчитать выплату в конкретный месяц, зная начальную (S) и конечную сумму (S₁)? Мы знаем, что долг увеличивается на p%, то есть становится aS. Если выплата равна x, то aS - x = S₁ ⇒ x = aS - S₁. Тогда:
1 выплата: долг = 100 - 5 = 95 руб., выплата = 100a - 95 руб.;
2 выплата: долг = 95 - 10 = 85 руб., выплата = 95a - 85 руб.;
3 выплата: долг = 85 - 15 = 70 руб., выплата = 85a - 70 руб.;
4 выплата: долг = 70 - 20 = 50 руб., выплата = 70a - 50 руб.;
5 выплата: долг = 50 - 25 = 25 руб., выплата = 50a - 25 руб.;
6 выплата: долг = 25 - 25 = 0 руб., выплата = 25a руб.
Сумма выплат: 100a - 95 + 95a - 85 + 85a - 70 + 70a - 50 + 50a - 25 + 25a = 100a + 95(a - 1) + 85(a - 1) + 70(a - 1) + 50(a - 1) + 25(a - 1) = 100a + (a - 1)*(95 + 85 + 70 + 50 + 25) = 100a + 325(a - 1) = 425a - 325 = 25(17a - 13) = 134 ⇔ 17a - 13 = 5,36 ⇔ 17a = 18,36 ⇔ a = 1,08 ⇒ p = 8%
ответ: 8%