15 б
методом индукции докажите, что при n∈n, значение выражения 13^n+ 5 кратное 6.
Другие вопросы по теме Алгебра
Популярные вопросы
- 5. На перекладине с концами в точках А и В в точке С сидит птица. Какова...
1 - БУДЬ ЛАСКА!! текст на англійській мові на тему поїздки у Львів. по абзацах...
1 - Listening Task 1. Are the sentences true or false? 1. The customers want...
2 - 2.Заполните таблицу: Химическая Тип химической Схема образования связи формула...
3 - 6. Природну воду від піску можна очистити: а) відстоюванням; б) випарюванням;...
3 - Упростить выражение (х-2)(х²+х-1)-х²(х-1)...
1 - До іть як можна скоріше будьласка....
1 - До іть будь-ласка 4. Що зумовило занепад держави Великих моголів ? 6. Як...
2 - Вибери правильні твердження про гідросферу....
2 - Вирази які не містять інших дій як додавання , віднімання ,множення піднесеня...
1
1) Базис индукции: n = 1
2) Предположим, что и для n = k выражение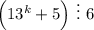
3) Индукционный переход: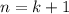
Первая скобка делится на 6 по предположению (второй пункт), ну а второе слагаемое делится на 6, поскольку выражение содержит сомножитель 12, следовательно,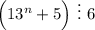 для всех натуральных
для всех натуральных