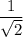14б! найдите минимальное значение ( дробь):
1/√(1+sin^(2)x))
ответ корень 2/2. мне нужно !
Другие вопросы по теме Алгебра
Популярные вопросы
- Write a topic about different types of musical instruments....
1 - перевести на украинский и поставить в правильном порядке надо здать до четырёх...
3 - Напишите мини эссе на тему: Важнейшее свойство почвы- плодородие ....
3 - Англійська мова за 6 клас. ...
1 - Как зделать 9a2-24ab+16ab2(кто ответит )...
2 - Яка кількість атомів гідрогену в молекулі насичиного вуглеводню який містить...
2 - Найти частные производные второго порядка функции:...
2 - Поясніть, як будова пір я пов язана з його функціями...
3 - дам. Частота змінного струму, який виробляє генератор , 300 Гц. З якою частотою...
3 - Оның бір жақсы қасиеті-адалдығы. Қияға қатысты ерік бермеген жөн. Көкейде жүрген...
3
Синус изменяется в пределах от -1 до 1. Оценим в виде двойного неравенства
Переворачивая дроби, мы меняет знаки неравенств
Наименьшее значение выражения равно