14. Найти действительные корни уравнения
x6 - 33x4 + 6x3 + 297x2 – 729= 0.

Другие вопросы по теме Алгебра
Популярные вопросы
- Написать 3 предложения о любой птице...
3 - Написать мини рассказ на тему „тебе на голову упала пластиковая бутылка.твои...
1 - Спиши текст,вставляя слово ягода в ноужном падеже. мы часто ходим в лес...
2 - Правильно написал? ,,рожков, к доске! - сказал учитель по ....
3 - Нужно мини сочинение по на тему safe our planet ответы будут проверяться...
3 - Как определяется спряжение глагола с приставкой вы...
2 - Длина школьного спортзала равна 15 м, а ширина 12 м. девятую часть площади...
1 - Строение и функции органа равновесия...
1 - Составьте предложение на схему а: п!...
3 - Скільки кілограмів сушених грибів отримують з 18 кг свіжих,якщо з 12...
1
(см. объяснение)
Объяснение:
Так как не является корнем уравнения, то поделим его на
не является корнем уравнения, то поделим его на  :
:
Выполним замену вида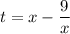 .
.
Тогда получим уравнение:
По формуле Кардано:
Обратная замена:
Решая это уравнение, получаем ответ:
Уравнение решено!