134 Площадь прямоугольного треугольника равна 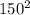. Найдите длины сторон треугольника, если они составляют арифметическую прогрессию

Будем считать, что площадь равна 150 кв.ед.

Пусть один катет равен x, второй x + a, гипотенуза x + 2a.

При двух неизвестных надо составить 2 уравнения.

Первое по Пифагору.

x² + (x + a)² = (x + 2a)².

x² + x² + 2ax + a² = x² + 4ax + 4a².

x² - 2ax - 3a² = 0.   D = 4a² - 4*1*3a² = 16a².  √D = 4a.

x₁ = (2a - 4a)/2 = -a  (отрицательное значение не принимаем).

x₂ = (2a + 4a)/2 = 3a.

Второе по площади: (1/2)*x*(x + a) = 150.

x² + ax = 300. Вместо х подставим 3a.

9a² + 3a² = 300.

12a² = 300,   a² = 300/12 = 25, a = √25 = 5.

Отсюда находим стороны треугольника.

х = 3а = 3*5 = 15.

х + а = 15 + 5 = 20.   Это катеты.

Гипотенуза равна 15 + 2*5 = 25.