Α = –1287° является углом 2 четверти -1287° = -360° * 3-207°. Что значит эти числа как "3" и "-207". Как их нашли, и как четверть нашли, напишите попродобней

Ответы

elizaveta4256 12.02.2021 11:00

Единичная окружность - это окружность с центром в начале декартовой системы координат, точке О(0;0) и радиуса, равного 1 , R=1 .

Точка Р(1;0) лежит на пересечении единичной окружности и оси ОХ. Это начало отсчёта углов. Если эта точка движется по окружности против часовой стрелки и займёт положение Р₁ , то это считается положительным направлением. Угол , образованный радиус-вектором ОР₁ и положительным направлением оси ОХ, будет положительным. Если эта точка движется по окружности по часовой стрелке, то это считается отрицательным направлением. Указанный угол будет отрицательным.

Так как угол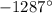 $-1287^\circ$ отрицательный, то поворот радиус-вектора ОР надо делать ПО часовой стрелке.

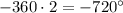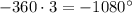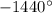Один полный оборот ПО часовой стрелке составляет $-360^\circ$ , два оборота составляют $-360\cdir \cdot 2=-720^\circ$ , три оборота составляют $-360\cdir \cdot 3=-1080^\circ$ . Если сделать ещё один оборот, то есть 4 раз повернуть ОР на $-360^\circ$ , то получим угол в $-1440^\circ$ , что меньше угла в 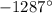$-1287^\circ$ . Значит , чтобы получить заданный угол , надо повернуть радиус-вектор ОР по часовой стрелке на 3 полных оборота и ещё на 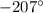$-207^\circ$ , так как

$-1287^\circ-3\cdot (-360^\circ )=-1287^\circ +1080^\circ =-207^\circ$ .

Тогда точка займёт положение Р₁ .

То есть имеем: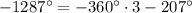 $-1287^\circ=-360^\circ \cdot 3-207^\circ$ .

Число 3 - это количество полных оборотов радиус-вектора ОР по часовой стрелке, а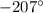 $-207^\circ$ - это количество градусов, которые нужно ещё добавить, чтобы получить 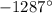$-1287^\circ$ . Получили, что угол лежит во 2 четверти .

Смотри рисунки .