11!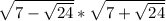

Объясните , как это решать. Заранее

ответ:  5.

Объяснение:

√a*√b=√ab.

Вносим произведение под один корень:

√(7-√24)*(7+√24) =>  разность квадратов двух выражений=>

=> √7²-(√24)²=√49-24=√25=5.

Здравствуйте!

5

Объяснение:

Нужно знать одно из свойств корней:

Ещё стоит вспомнить про формулу сокращенного умножения, а именно разность квадратов:

Переходим к решению: