100 б + лучший ответ! тригонометрия, найти область определения (с подробным решением):
Другие вопросы по теме Алгебра
Популярные вопросы
- Сколько тепла надо отнять от 3 кг стоградусной воды,чтобы получить лед с температурой...
2 - You got a letter from friend alex, who lives in norwich. he asks you to write...
3 - вычислите массовую долю азота в азотстой кислоте дано найти и решение...
1 - Страны африки расположенные частично на равнинах, частично в горах...
1 - Втреугольнике abc, ab=10см, ac=12см, угол а=45 градусов...
3 - Перечислите основные условия эффективному обмену информацией и осуществлению...
1 - Назовите основные черты сходства и различия промышленности, сельского хозяйства...
1 - They re new pupils and i don t know ( their/theirs)names (my/mine) fiat is...
2 - Нужны 10 вопросов о независимости казахстана(на казахском)...
2 - Напишите небольшой текст на одну из следующих тем на перемене употребите наряду...
2
ответ: ∈
∈ ![[-5 ; -\sqrt{3}]](/tpl/images/1008/3859/da582.png) ∪
∪ ![[\sqrt{3};5]](/tpl/images/1008/3859/34029.png)
Объяснение:
Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.
Для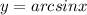
 ∈
∈![[-1 ; 1]](/tpl/images/1008/3859/dff6b.png)
Для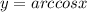
 ∈
∈![[-1 ; 1]](/tpl/images/1008/3859/dff6b.png)
Решаем систему:
Четыре уравнения.
1)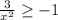 ⇒
⇒ 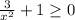
Выполняется для любых .
.
2)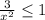 ⇒
⇒ 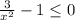 ⇒
⇒
Дробь может быть меньше либо равно нулю тогда и только тогда, когда ее числитель неотрицателен, а знаменатель отрицателен, либо когда ее числитель отрицателен или равен нулю, а знаменатель положителен, т.е. в первом случае:
Во втором случае:
3)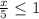 ⇒
⇒ 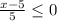 ⇒
⇒ 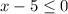 ⇒
⇒ 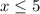
4) Аналогично третьему уравнению находим:
Находим пересечение всех полученных промежутков:
1) ∀
2) ∈
∈ ![(-\infty;-\sqrt{3}]](/tpl/images/1008/3859/aebdf.png) ∪
∪ 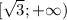
3)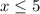
4)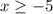
ответ: ∈
∈ ![[-5 ; -\sqrt{3}]](/tpl/images/1008/3859/da582.png) ∪
∪ ![[\sqrt{3};5]](/tpl/images/1008/3859/34029.png)