1. Алгебра
  2. 1. Знайдіть суму перших

1. Знайдіть суму перших шістнадцяти членів арифметичної прогресії, якщо її перший та шістнадцятий члени дорівнюють 3; і -5 2. Знайдіть суму перших шістнадцяти членів арифметичної прогресії, якщо її перший член дорівнює 6, а різниця дорівнює 3

3. Знайдіть суму перших сорока семи членів арифметичної прогресії, яку задано ось такою формулою загального члена аn=3n-1

4. Знайдіть суму членів арифметичної прогресії, якщо виключно з 6 по 23, якщо її перший член дорівнює 28, а п'ятий дорівнює 16

znayka141 znayka141    3   02.08.2022 01:22    0

Ответы
MorozilkAAA MorozilkAAA  02.08.2022 01:23

1. –16;

2. 456;

3. 3337;

4. –225

Объяснение:

1. Пользуемся формулой суммы арифметической прогрессии

{S_n} = \displaystyle\frac{{{a_1} + {a_n}}}{2} \cdot n,

где n = 16, {a_1} = 3, {a_{16}} = - 5.

{S_{16}} = \displaystyle\frac{{3 - 5}}{2} \cdot 16 = - 16.

2. Пользуемся формулой суммы арифметической прогрессии

{S_n} = \displaystyle\frac{{2{a_1} + d(n - 1)}}{2} \cdot n,

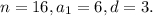
где n = 16, {a_1} = 6, d = 3.

{S_{16}} = \displaystyle\frac{{2 \cdot 6 + 3(16 - 1)}}{2} \cdot 16 = 456.

3. Найдем 1-й и 47-й члены этой последовательности:

{a_1} = 3 \cdot 1 - 1 = 2; {a_{47}} = 3 \cdot 47 - 1 = 140.

Далее применим формулу, указанную в п. 1:

{S_{47}} = \displaystyle\frac{{{a_1} + {a_{47{2} \cdot 47 = \displaystyle\frac{{2 + 140}}{2} \cdot 47 = 3337.

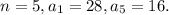
4. Подставим в формулу общего члена {a_n} = {a_1} + d(n - 1) значения n = 5, {a_1} = 28, {a_5} = 16.

16 = 28 + d(5 - 1), d = - 3.

Далее сумму членов с 6 по 23 найдем как разность сумм {S_{23}} - {S_5}. Каждую из сумм вычислим по формуле суммы из п. 2.

{S_{23}} = \displaystyle\frac{{2{a_1} + d(n - 1)}}{2} \cdot n = \displaystyle\frac{{2 \cdot 28 - 3(23 - 1)}}{2} \cdot 23 = - 115,

{S_5} = \displaystyle\frac{{2{a_1} + d(n - 1)}}{2} \cdot n = \displaystyle\frac{{2 \cdot 28 - 3(5 - 1)}}{2} \cdot 5 = 110,

{S_{23}} - {S_5} = - 115 - 110 = - 225.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
MrAlexCross MrAlexCross  20.01.2021 10:20
У-1/х+1/х³ y=1/2x²+5x-13 у=(9-х²)(х+2)найдите производную обешаю это...
dlimfam dlimfam  20.01.2021 10:20
1 задача Функция задана формулой y=-3x+6 на промежутке [1;2]. Изобразить график функции и указать по нему все целые значения, которые может принимать функция.2 задачаИзобразить...
elenafink69 elenafink69  20.01.2021 10:20
ответьте решите уравнение только с полным решение а не только ответ 1)x²-0,04=0 2) y²- 1 девятая (дробь) =0​...
m5zapir m5zapir  20.01.2021 10:20
27m9 + A = (3m3 + 2n2)(B – C + 4n4)​...
sleeplessness5 sleeplessness5  18.11.2020 17:11
Найти предел последовательности...
алекса146 алекса146  18.11.2020 17:11
Решите уравнение и напишите ход решений 8y-x/yx-1/y+x*(y/x-x/y)=7/x...
Дарья22012007 Дарья22012007  18.11.2020 17:11
Найдите значение выражения 5-3n/m-3n^2+5n/mn при m=8; n=3,2...
Фариза04 Фариза04  18.11.2020 17:11
Алгебра 9 класс,скай смарт...
regina290402 regina290402  18.11.2020 17:12
решите 2 варианта, с 1 по 6 задания, алгебра 11 класс...
Айхан11111111 Айхан11111111  18.11.2020 17:12
дано уравнение окружности х2 + у2 = 400 1)найли ординату точек на этой окружности, абсцисса которых 20. (запиши обе координаты точек, в точке А - ординату со знаком...

Популярные вопросы