1. Запишите квадратное уравнение, корни которого равна:
а) 2 и 5; б) - 1 и 3; в) 0,4 и 2,5 .
2. Найдите подбором корни уравнения:
а) х2 – 5х + 6 = 0 ; г) х2 – 3х – 10 = 0;
б) х2 + 8 х + 15 = 0; д) х2 – 17х + 42 = 0 ;
в) х2 – 8х – 9 = 0 ; е) х2 – 11х – 80 = 0 .
3. Один из корней квадратного уравнения равен 2. Найдите второй корень уравнения :
а) х2 + 17х – 38 = 0 ;
б) 7х2 – 11х – 6 = 0.
C РЕШЕНИЕМ!
Другие вопросы по теме Алгебра
Популярные вопросы
- Есептеулерді орында. 18/19-7/19+3/19=9/11-3/11-2/11=1/15-(3/15+7/15)= памаги...
1 - 40×(3 1/5-2 2/4) решение и ответ...
2 - у меня СОР по информатике ...
1 - Выразите через тригонометрические функции угла α: 1) tg(п/4 + α) 2) ctg(п/4...
1 - Составь и запиши в тетрадь план статьи учебника «Поэт, музыкант, человек-легенда...
2 - Выполнить 1) Вообразите, что ещё могла увидеть Золушка, и продолжите описание...
3 - Подчеркни слова которые обозначают действия предметов...
1 - 5. 5. Шамамен алынған сандары бар сөйлемдерді теріп жаз.1. Мен 7-8 түп қайың...
1 - Почему А. А Чехова можно назвать интелегентным? ...
1 - Для чего используется трассировка алгоритма дам 20б...
2
используем теорему Виета для решения всех заданий. Напомню, что по теореме Виета x1 + x2 = -p и x1 × x2 = q, где p и q коэффиценты уравнения x² + px + q = 0.
1. a) если корни равны 2 и 5, то p и q равны соответственно -7 и 10, подставляем их в исходное уравнение:
x² - 7x + 10 = 0, делаем все аналогично для пунктов б) и в):
б) x² - 2x -3 = 0
в) x² - 2,9x + 1 = 0
2. Подбором находим корни уравнений, затем делаем проверку:
а) 3; 2 3 × 2 = 6 и 3 + 2 = -(-5)
б) -3; -5 -3 × -5 = 15 и -3 - 5 = -8
в) 9; -1
г) 5; -2
д) 3; 14
е) 16; -5
3. Т.к. нам дан один корень, то можно найти второй через коэффицент q, а потом сделать проверку через коэффицент p:
a) 2 × x = -38, отсюда x = -19
проверим: -19 + 2 = -17, значит все правильно
б) поскольку это уравнение не приведенное, то разделим его на 7, чтобы сделать приведенным:
x² -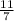 -
-  = 0
= 0
теперь мы можем сделать тоже, что и в пункте а):
2 × x = , отсюда х =
, отсюда х = 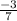
проверим: 2 - =
= 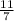
Все верно, значит мы решили правильно!