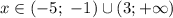1/x+1<2/x-3
решить, я вообще не понимаю.
Другие вопросы по теме Алгебра
Популярные вопросы
- Комедия горе вопрос: чем неожиданен для нас молчанин, диалог с чацким?...
2 - Двойка светит: (/-означает дробь) при каких значениях переменной дробь равна нулю:...
1 - Зробити проект на тему пригтуваня їжі + текст 1.що готувати2.ингредиєенти 3.приготуваня...
2 - Вот наступит зима,и пригодится тебе это 1)поделка,2)покупка,3)находка,4)новинка,5)обновка...
3 - 3найдите ошибку в словоупотреблении. а) первый снег б) первый в) первый класс г)...
3 - Индейцы северной америки ( ихние обычия ,традиции)...
3 - Учитель написал на доске слова: , , , - и попросил учеников вставить перед ними...
1 - Расставить знаки припенания 1)здесь люди как будто боятся знакомиться. 2)онегин...
2 - Какие цифры пропущены? 27: 6= ( ост. ) 32: 9= (ост. ) : 13=5 (ост.2) : 24=3(ост.6)...
3 - Как это решить? x^2+16x -63 и 4x^2+14x-56 меньше или равно (x+4)^2 нужно, заранее...
3
ответ: см фото.
Объяснение:
1) Сведем дробно-рациональное неравенство к виду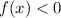
Домножим обе части неравенства на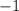 , при этом изменим знак неравенства на противоположный:
, при этом изменим знак неравенства на противоположный:
2) Найдем область допустимых значений (ОДЗ):
3) Найдем нули функции
4) Обозначим на координатной прямой нули и ОДЗ функции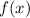 , найдем знак функции на каждом промежутке (см. вложение), подставляя из выбранного промежутка некоторое значение (знак "+", если
, найдем знак функции на каждом промежутке (см. вложение), подставляя из выбранного промежутка некоторое значение (знак "+", если 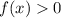 , и "–", если
, и "–", если 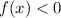 ).
).
5) Объединим все полученные промежутки со знаком "+", поскольку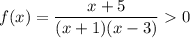
ответ: