1. Алгебра
  2. 1)Вычислите sin^4(3π/2− 2α)

1)Вычислите sin^4(3π/2− 2α) , если cos(π − 4α) = −1/3. 2)Упростите выражения sin 50 + 8 sin 10sin 50sin 70( в градусах)

Anal0l Anal0l    3   25.11.2020 19:43    1

Ответы
MATVEI235 MATVEI235  25.12.2020 19:44

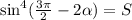
1) \sin^4( \frac{3\pi}{2} - 2\alpha) = S

\cos(\pi - 4\alpha) = -\frac{1}{3}

Используем формулу косинуса двойного аргумента:

\cos(2x) = \cos^2(x) - \sin^2(x) = 1 - \sin^2(x) - \sin^2(x) = 1 - 2\sin^2(x)

тогда

\sin^2(x) = \frac{1 - \cos(2x)}{2}

тогда

S = (\sin^2(\frac{3\pi}{2} - 2\alpha))^2 = (\frac{1 - \cos(3\pi - 4\alpha)}{2})^2 =

= (\frac{1 - \cos(\pi - 4\alpha)}{2})^2 = (\frac{1 - (-\frac{1}{3})}{2})^2 =

= (\frac{1+\frac{1}{3}}{2})^2 = (\frac{3+1}{2\cdot 3})^2 = (\frac{4}{6})^2 =

= (\frac{2}{3})^2 = \frac{4}{9}

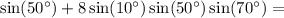
2) \sin(50^\circ) + 8\sin(10^\circ)\sin(50^\circ)\sin(70^\circ) =

= \sin(50^\circ)\cdot ( 1 + 8\sin(10^\circ)\sin(90^\circ - 20^\circ) ) =

= \sin(50^\circ)\cdot (1 + 8\sin(10^\circ)\cos(20^\circ) ) =

= \sin(50^\circ)\cdot (1 + \frac{8\sin(10^\circ)\cos(10^\circ)\cos(20^\circ)}{\cos(10^\circ)}) = V

Используем формулу синуса двойного аргумента:

\sin(2x) = 2\sin(x)\cos(x)

V = \sin(50^\circ)\cdot (1+ \frac{4\sin(20^\circ)\cos(20^\circ)}{\cos(10^\circ)}) =

= \sin(50^\circ)\cdot (1 + \frac{2\sin(40^\circ)}{\cos(10^\circ)}) =

= \sin(50^\circ) + \frac{2\sin(50^\circ)\sin(40^\circ)}{\cos(10^\circ)} = W

Используем формулу "произведение синусов":

2\sin(\alpha)\sin(\beta) = \cos(\alpha - \beta) - \cos(\alpha + \beta)

W = \sin(50^\circ) + \frac{\cos(50^\circ - 40^\circ) - \cos(50^\circ + 40^\circ)}{\cos(10^\circ)} =

= \sin(50^\circ) + \frac{\cos(10^\circ) - \cos(90^\circ)}{\cos(10^\circ)} =

= \sin(50^\circ) + \frac{\cos(10^\circ) - 0}{\cos(10^\circ)} =

= \sin(50^\circ) + 1.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Vilaan1972 Vilaan1972  15.02.2022 07:03
Решение задачу с уравнения . ширина прямоугольника на 5см меньше длины , а его площадь 14 см2. найдите стороны и периметр прямоугольника...
Айдана55л Айдана55л  15.02.2022 07:04
ПО 1. Тело брошено вертикально вверх. Высота (ht), на которой находится тело через 1 секунд полета, Вычисляется формуле h = -0,5gt? + vot+ho где gе 10 (м/с), vo начальная...
Ника12040000 Ника12040000  15.02.2022 07:06
Маятников Чему равна жесткость пружинного маятника, который изображен на графике, если масса груза 2 кг?4,9Н/м....
natalicharry natalicharry  15.02.2022 07:09
10 класс. Сумма всех членов убывающей геометрической прогрессии равна (-17,5), а знаменатель этой прогрессии равен 0,6. Найдите третий член этой последовательности....
ЛамповыйКун1 ЛамповыйКун1  15.02.2022 07:13
2) [6] Теплоход, собственная скорость которого 18 км/ч 10 км по течению реки и 16 км против течения, затратив на весь путь 1 час 30 минут. Какова скорость течения реки?...
Zheka5644 Zheka5644  15.02.2022 07:14
A) (12 - x)/(x ^ 2 - 9) = (x ^ 2)/(x ^ 2 - 9) 6) 5/(x - 3) - 8/x = 3 2. H_{3} пункта А в пункт В велосипедист проехал по дороге длиной 48 км, обратно он возвращался по другой...
animator351 animator351  15.02.2022 07:15
ЛЮДИ ДОБРЫЕ Разложите на множители многочлен:а) y²-10у+25б) 9х²-49/144в) у²-5у+4г) х²-х-6д) 2х²-7е)у²+7у-8СДЕЛАйТЕ ХОТЬ НЕМНОГО...
Karamy33 Karamy33  20.09.2019 06:20
Как построить график функции прямой пропорцианальности y=3x...
Dayanna01 Dayanna01  20.09.2019 06:20
Надо избавиться от иррациональности 12 }это дробь 7√3...
Milana2K18 Milana2K18  20.09.2019 06:20
Выражение и вычислите его значение при а= –2 3а(а 2-а+1)-0.5а 2(4а-6)=...

Популярные вопросы