1)скорость гоночного автомобиля,движущегося прямолинейно,изменяется по закону v(t)=4t^3 2)ускорение гоночного автомобиля в момент времени t=2 равно.. варианты ответов а-46 б-28 в-12 г-45 3)скорость гоночного автомобиля на тарссе контролируется 4 камерами через определенное время от начала движения,устаноаите соответствие между временем и скоростью передвежения гоночного автомобиля 1.t=1 2.t=2 3.t=3 4.t=5 варианты ответов 1)2 2)28 3)102 4)490 5)253 3 время гоночного автомобиля при котором ускорение a=46 равно.. 4 путь пройденный гоночным автомобилем за 5 с от начала движения равен..

Условие подправлю: скорость гоночного автомобиля,движущегося прямолинейно,изменяется по закону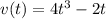

Производная от скорости есть ускорение

a(t) = v'(t) = 12t² - 2

ускорение гоночного автомобиля в момент времени t=2 равно

a(2) = 12 * 2² - 2 = 2*(24 - 1) = 2 * 23 = 46

3) v(1) = 4 * 1³ - 2 * 1 = 4 - 2 = 2

v(2) = 4 * 2³ - 2 * 2 = 28

v(3) = 4 * 3³ - 2 * 3 = 102

v(5) = 4 * 5³ - 2 * 5 = 490

задание 3

время гоночного автомобиля при котором ускорение a=46 равно..

46 = 12t² - 2

48 = 12t²

t² = 4

t=2.

4) Обратное действие производной скорости есть путь(первообразная)

1) Для определения ускорения автомобиля в момент времени t=2, нужно взять производную скорости по времени: a(t) = dv(t)/dt.
Производная функции v(t) = 4t^3 равна:
a(t) = 12t^2

Заменяем t на 2:
a(2) = 12(2)^2 = 12(4) = 48

Таким образом, ускорение автомобиля в момент времени t=2 равно 48.

2) Для определения соответствия между временем и скоростью, нужно подставить значения времени в функцию скорости v(t) и найти соответствующие значения скорости.

a) При t=1:
v(1) = 4(1)^3 = 4

b) При t=2:
v(2) = 4(2)^3 = 4(8) = 32

c) При t=3:
v(3) = 4(3)^3 = 4(27) = 108

d) При t=5:
v(5) = 4(5)^3 = 4(125) = 500

Таким образом, соответствие между временем и скоростью будет:
1) Скорость 2 при времени 1
2) Скорость 32 при времени 2
3) Скорость 108 при времени 3
4) Скорость 500 при времени 5

3) Для определения времени, при котором ускорение a=46, нужно решить уравнение a(t) = 46:

12t^2 = 46

Делим обе части уравнения на 12:
t^2 = 46/12
t^2 = 3.8333

Извлекаем квадратный корень:
t = √(3.8333)

Таким образом, время, при котором ускорение a=46, будет приближенно равно 1.958

4) Чтобы определить путь, пройденный гоночным автомобилем за 5 секунд от начала движения, нужно найти интеграл от скорости v(t) на интервале времени от 0 до 5:

∫[0,5] 4t^3 dt

Интегрируем по степени t:
∫[0,5] 4t^3 dt = (4/4)t^4 | [0,5]

Подставляем верхний и нижний пределы интегрирования:
(4/4)(5^4 - 0^4) = 5^4 = 625

Таким образом, путь, пройденный гоночным автомобилем за 5 секунд от начала движения, равен 625 метров.