1) скорость движения точки: v=(9t^2-8t) m\c. найти путь, пройденный точкой за четвертую секунду. 2) найти площадь фигуры, ограниченный линиями: y = 2x y = 0, x=4
Другие вопросы по теме Алгебра
Популярные вопросы
- В историческом музее случайно перепутались экспонаты трёх отделов:...
1 - Китайцу Чжану Хэну принадлежит изобретение очень нужного прибора. Более...
3 - Определите, какой из отрывков относится к древнеиндийской поэме, а...
1 - Пользуясь картой параграфа и картой из атласа по истории Древнего мира,...
1 - Веер придумали в Древнем Китае. По словам журналиста-востоковеда В.С.Куликова,...
1 - Составьте план рассказа о морском путешествии древних греков, используя...
3 - На основе пункта «Повседневная жизнь в Древней Индии» выработайте правила...
2 - Определите, какой исторический источник перед вами (закон, художественный...
2 - Прочитайте текст, написанный одним из древних египтян. Какие достоинства...
2 - Рассмотрите иллюстрации на с. 24 рабочей тетради. Какая из них относится...
3
Вначале заметим, что первообразная скорости равна пройденному пути, откуда имеем следующее:
Для того, чтобы найти путь, пройденной точкой за четвертую секунду, найдем путь, который точка за четыре секунды и за три секунды, а затем из первого вычтем второе.
Считаем разность:
ответ: точка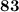 метра за четвертую секунду.
метра за четвертую секунду.
2).Для нахождения площади этой фигуры можно, во-первых, воспользоваться формулой Ньютона-Лейбница для вычисления интегралов:
В нашем случае (если приравнять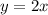 и
и 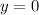 )
) 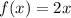 .
.
Найдем сам интеграл:
Можно было пойти по-другому: изобразить все на координатной плоскости (смотрите вложенный файл) и по формуле площади прямоугольного треугольника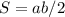 найти площадь
найти площадь 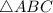 :
:
В обоих случаях получился одинаковый ответ!
ответ: площадь фигуры равна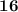 .
.