1. sin6x/cos8x=-1 2. sin12x/sin8x=-1
Ответы
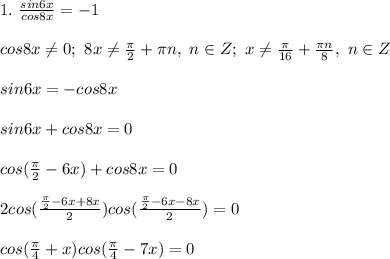
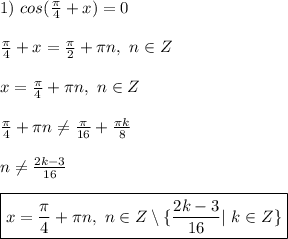
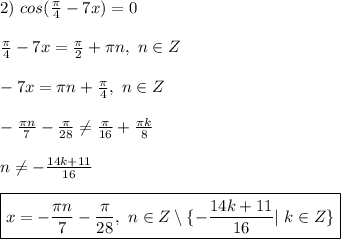

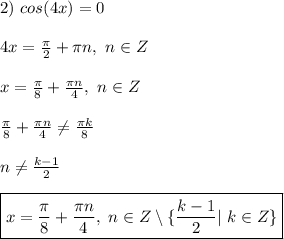
Другие вопросы по теме Алгебра
Популярные вопросы
- Проведите реакцию галогенирования 3-изопропил-октана...
2 - Слово копировать одназначное или многозначное ? докажите составив словосочитание...
1 - Розібрати як частину мови слова: славу, сором, матері, простоту...
1 - Сколько цифр содержится в произведении чисел 30 и 700? вычислите периметр прямоугольника...
1 - Если к числу 360 прибавить частное x и 3 , то получится 440. если частное x и 8...
3 - Подготовить сообщение о традициях семьи...
3 - Отгадайте омоним по его значениям: 1)животное,2)бег лошади....
3 - :подчеркнуть слова с беглыми гласными. обозначь морфемы, в которых они находятся....
3 - Аня прочитала за 6 минут 4 страницы книги. сколько страниц она прочитает за час....
2 - Поэма дедушка почему отец и мать не хотели ответить на сашин вопрос где дедушка?...
2