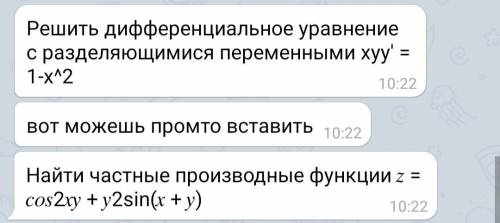
1. Решить дифференциальное уравнение с разделяющимися переменными xyy' = 1-х^2 2. Найти частные производные функции (на фото продолжение)
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите . найти высоту пирамиды если ее основанием является прямоугольник...
1 - Укажите, для какого из указанных значений х истинно высказывание (x 10)...
3 - Какова основная причина восстания гладиаторов в риме в 74 году до нашей...
3 - Собственная скорость теплохода 27 км/час , скорость течения реки 3 км/час...
3 - На конденсаторе написано 100 пф и 300 в какой заряд можно накопить на...
2 - Какую сказку подарил эгль девочке? (алые паруса)...
1 - Определите длины волн, соответсвующих движению альфа-частицы со скоростью...
1 - Какие основные органы растения и их значение в жизни скорее, заранее !...
2 - Вдетском мире продавали трехколёсные и двухколесные велосипеды . вася...
2 - Выполните действия. (-5,8)в квадрате-14,28 умножить (-5/7)-30.04...
1
1.
общее решение
2.