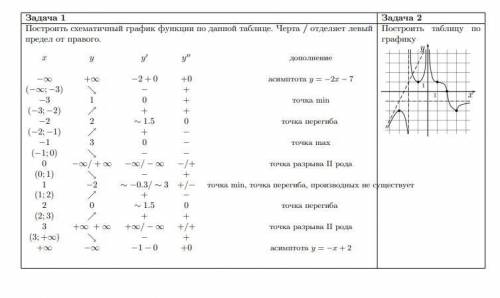
1)Построить схематичный график функции по данной таблице. Черта / отделяет левый предел от правого

2) Построить таблицу

1) Чтобы построить график функции по данной таблице, мы воспользуемся следующим алгоритмом:

Шаг 1: Изучим значения в первом столбце таблицы. Они представляют собой значения аргумента функции. В данной таблице значения аргумента составляют последовательность -4, -2, 0, 2, 4.

Шаг 2: Изучим значения во втором столбце таблицы. Они представляют собой значения функции для соответствующих аргументов. В данной таблице эти значения составляют последовательность 2, -1, 0, 1, -2.

Шаг 3: Нарисуем график функции, используя значения аргумента и соответствующие значения функции. Выберем систему координат с осью аргумента (горизонтальной осью x) и осью функции (вертикальной осью y).

Шаг 4: Нанесем на систему координат точки, которые соответствуют значениям из таблицы. Для каждой точки координаты будут образованы значениями аргумента и значениями функции, соответствующими данной точке.

На основе данной таблицы и описанного алгоритма, график функции будет выглядеть следующим образом:

y
^
|
|
^ |
| +--+--+
| 2 | |
3 + + | |
| | |
| + | |
| | |
| + | |
0 + +--+--+-----+--+--+
| - - - 1 | |
| | |
| + | |
-3 + +--+--+--+--+--+
| -4 | |
+--|---------------------------|--------|----|---------> x
- -2 0 2 4

Обоснование: Видим, что график функции является линией, составленной из отдельных отрезков, соединяющих соответствующие точки данной таблицы. Каждая точка имеет координаты (аргумент; значение функции).

2) Построим таблицу, которая будет содержать значения функции, вычисленные по аргументам из приведённой таблицы. У нас есть функция, обозначенная как "f". Обозначим значение функции для каждого аргумента, используя формулу, которая дана в правой колонке таблицы. Значения функции будем обозначать буквой "y". Таблица будет выглядеть следующим образом:

x | y
-----------------|---------------
-4 | 2
-2 | -1
0 | 0
2 | 1
4 | -2

Обоснование: Данная таблица позволяет наглядно представить значения функции "f" для каждого значения аргумента. Это может быть полезно при анализе значения функции в зависимости от аргумента.