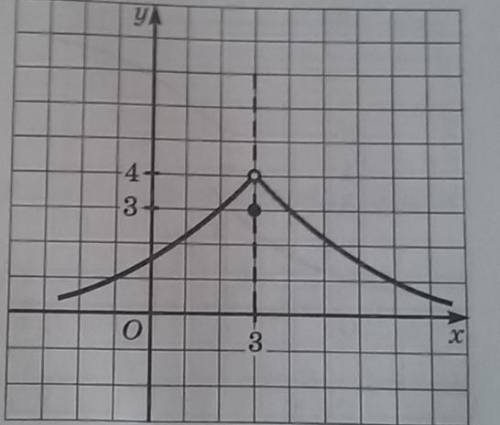
1) По графику найдите предел функции Lim x → 3 f(x)
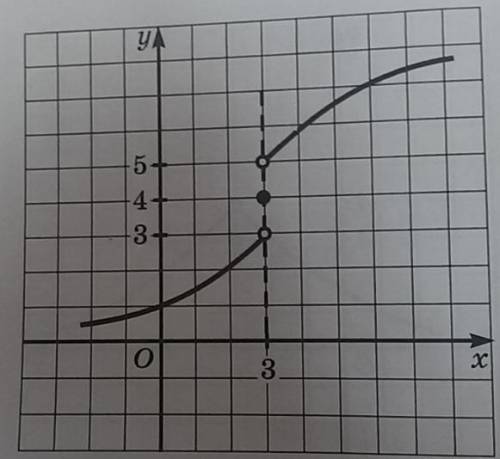
2) По графику найдите предел функции Lim x → 3 f(x)

Здравствуйте!

Для того чтобы найти предел функции Lim x → 3 f(x), нужно оценить поведение значения функции f(x) при стремлении x к 3.

1) По графику первой функции, видно что при x, близком к 3, значение функции f(x) достаточно стабильно и равно 5. Это можно сделать выводя из того, что на графике в окрестности точки x=3 соответствующее y-значение равно 5. Поэтому можно утверждать, что предел функции Lim x → 3 f(x) равен 5.

2) По графику второй функции, видно, что при x, близком к 3, значение функции f(x) неустойчиво и колеблется между -2 и 2. Так как предел функции существует только при стремлении значения x к конкретной точке, а не приближении с разных сторон, как в данном случае, где функция изменяет свое значение вокруг точки x = 3, мы не можем однозначно определить значение предела.

Второй график не позволяет нам однозначно сказать, что предел функции Lim x → 3 f(x) существует и равен определенному значению.

Вернитесь, если у вас возникли еще вопросы. Я всегда готов помочь!