1)Освободиться от иррациональности в знаменателе дроби: \\ ![\frac{a - 1}{\sqrt{a} - \sqrt[3]{a}} = \\](/tpl/images/3785/3126/7cb6b.png)
2) показать, что если ![z = \sqrt[3]{a + \sqrt{a^{2} + b^{3}}} - \sqrt[3]{\sqrt{a^{2} + b^{3}} - a}](/tpl/images/3785/3126/73257.png) , тогда
, тогда 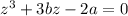
3) Упростить выражение: (Представить в виде суммы трёх радикалов.)
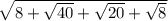
Другие вопросы по теме Алгебра
Популярные вопросы
- ACTIVATE Complete the sentences about your diet. Discuss how healthy or unhealthy...
2 - Запиши число 8 единиц 7 разряда, 5 единиц 5 разряда, 9 единиц 4 разряда,...
2 - Записать 12 предложений +-?используя конструкцию Used to+infinitive (выбранное...
1 - Қазақ орыс қатынастарынын басталуының алғы шарттары туралы аитындар...
3 - Рассчитайте массовую долю элементов в диоксиде серы SO2...
3 - Объясните причину подобного химического проведения кобальта...
3 - Lesson 2 a) 1. Complete the crossword. Across 4. Something that is difficult,...
2 - Замените словосочетание « бегающий быстро», построенное на основе управления,...
1 - Используя свойства функции для у=корень х заполните таблицу для функиии у=...
2 - Экологилық пирамида деген не...
1
1)
Поскольку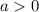 , для удобства преобразований обозначим:
, для удобства преобразований обозначим:
2)
Обозначим:
Тогда:
3)
Внутри радикала проглядывается формула квадрата суммы трех слагаемых: