1. Определите первые три члена арифметической прогрессии по заданным данным: {a2+a4=16
{a1*a5=28
Другие вопросы по теме Алгебра
Популярные вопросы
- фото в файле. Перед отправкой напишите процент правильности вашего...
2 - доходность инвестиций в 2005 году составил 12% определить реальную...
2 - Вариант 1Вопрос 1:Электростанции, снабжающие потребителей только...
2 - ∆ ABC B-BC BD- высота,BD-8 см AC-12 см AB-?...
1 - Ребят ищу задания для второго варианта Контрольна робота No3...
1 - Выбери три верные утверждения. (Запиши в ответе цифры в порядке...
1 - Портниха2)Доярка3)стоматолог 4)няня,воспитатель 5)учитель 6)ботаник7)писатель,журналист...
1 - какие прямые измерения и какие косвенные нужно выполнить для...
1 - В магазин поступила новая продукция с трех предприятий. Процентный...
3 - КАПЕЦ КАК ПРЯМ нужно придумать соченение с разносклоняемыми существительными...
2
Два варианта первой тройки членов ар. прогрессии.
Объяснение:
Для арифметической прогрессии справедливо
Нам известно:
Выразим а2, а4, а5 через а1 и b:
То есть для первого равенства:
Для второго:
Запишем это в системе:
Решим 1 уравнение системы
Отсюда:
То есть имеем 2 варианта решения:
1)и такие первые три члена арифм.прогрессии:
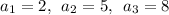
2)и такие первые три члена арифм.прогрессии
ПРОВЕРКА:
1) Если а1 = 2, b = 3:
2) Если а1 = 14, b = -3: