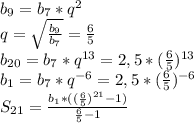1. найти формулу n-го члена и b_10 следующей прогрессии:
-0,7; -1,4; -2,8; …
2. задана следующая прогрессия: 75; 15; 3; … найти b_8 и сумму бесконечно убывающей прогрессии?
3. дано b_7=2,5 и b_9=3,6. найти b_20 и s_21?
Другие вопросы по теме Алгебра
Популярные вопросы
- Побудуй прямокутник зі сторонами 12см і 3 см Розріж його на 4 рівні частини...
3 - 1 + 3/15= 1-11/15= 16/15-1= 8/15+1=...
2 - с русским Глаголы изменяются: 1) по падежам и родам; 2) временам и числам;...
1 - Выбери из следующих слов типы устья рек. * паводок дельта водопад порог...
2 - ОЧЕНЬ Поводом к Столетней войны стало... 1)Желание католической церкви расширить...
3 - А10 Какая функция свойственна образованию?1) приобщение человека к культуре...
3 - Побудувати трикутник amc за до циркуля і лінійки якщо mc=3 am=5 ac=7. опишить...
2 - Гасло “Хліба й видовищ” пов’язане з ??? А) гладіаторськими боями Б) театральними...
2 - Популяция животных – это:А) число особей на единицу площадиБ) число особейВ)...
1 - Произведения какого вида искусства имеет трехмерный объем: архитектура,...
3
Объяснение:
1)
2)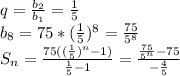
3)