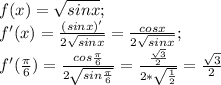1.найдите производную функции y=x cos x в точке х нулевое= пи. 2.найдите производную функции y= in cos x я думаю,что в первом случае y= 1 sin 1, мне кажется это неправильно.. а во втором 1/ sin x. а вот в третьей вообще не разберу ничего: f(x)= корень из sin x в точке х нулевое равно пи на 6. нужно найти значение буду признательна за ответ)
Другие вопросы по теме Алгебра
Популярные вопросы
- Прочитайте поэму А. А. Ахматовой Реквием . Какие ощущения она...
2 - Какие животные и растения неприжились в самарской области...
1 - Решите ЗАрание Упражнение 1. Раскройте скобки. Там, где нужно,...
1 - 20 ballov Из предложений 5–14 выбери сложное(-ые) предложение(-я)...
2 - Знайти градусну міру кожного з двух внутрішніх односторонніх...
1 - На основе статьи придумайте и расскажите фантастическую историю...
1 - Решите англиский терминасова 2 часть 48 стр...
2 - 4 тапсырмаға көмектесіңіздерші өтініш!...
3 - Русский Язык. Файл прикрелю...
3 - Тест по физике 9 класс1)Какая физическая величина является мерой...
3
1.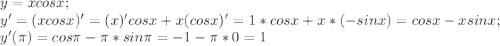
2.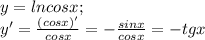
x0 для второго случая не указано
3.