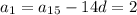1)найдите первый член и разность арифметической прогрессии (an) , если a9+a7=70 a5-a2=15 2) найдите сумму первых 12 членов арифметической прогрессии, заданной формулой an=7-3n 3) в арифметической прогрессии (аn) а15= -1,5, а6= три четвертых. найдите а4+а7 за ранее огромное )
Другие вопросы по теме Алгебра
Популярные вопросы
- Периметр равнобедренного треугольника АВС с основанием АС равен 12 см,...
3 - 6. Тас және қола дәуірлерін салыстырып, сипаттама беріңдер. Салыстыруға...
2 - 33.22. Какова будет длина стороны квадрата, изготовленного из проволоки...
3 - Use Present Perfect. Образуйте Настоящее совершенное время. She the dishes....
2 - У котрому рядку всі займенники належать до одного розряду? У котрому...
3 - Функция задана формулой y=2,5x, постройте её график и определите : a)значение...
3 - Task 3. Use the where necessary. 1. Wales is a part of United Kingdom....
3 - Вычислите количество вещества 4 литров кислорода. С дано: решение. За...
3 - Поділити на слоги . Для недільних шкіл Т. Г. Шевченко в 1861р. написав...
1 - Анализ ПОПС «Если национальный код, национальная культура не сохранится,...
3
1. Используя формулу n-го члена арифметической прогрессии: an = a1 + (n-1)d, решим следующую систему уравнений
***************************************************************************************************
2.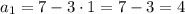
Имеем арифметическую прогрессию с первым членом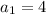 и разностью прогрессии
и разностью прогрессии 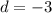
Сумма первых 12 членов арифметической прогрессии, равна:
**************************************************************************************************
3. Разность прогрессии: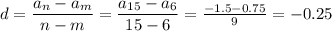
Первый член арифметической прогрессии: