1) Найдите периметр четырёхугольника с подробным решением
Перепутал это геометрия
Другие вопросы по теме Алгебра
Популярные вопросы
- Для варенья взяли 2 части смородины,1 часть малины и 4 части сахара.оказалось,что...
3 - Найдите площадь полной поверхности правильной треугольной призмы сторона основания...
1 - Найдите область значений функции y = -7sin3x...
1 - Решите : туристы проехали 60 км,что составило 23 всего пути.найдите длину всего...
2 - Вычислить сумму 1+1/2+ 1/3 +.. +1/n по с# только цикл...
1 - Перечислите события, которые пережила ахматова в течение жизни....
3 - А1. ученые используют понятие общество для характеристики. 1) результатов деятельности...
2 - Что изучают технические науки? что исследуют общественные науки?...
3 - Длина туристисескава маршрута 48 км в первый день туристы третью часть всего маршрута...
1 - Пользователь вводит число,программа должна вывести на экран 3 случайных числа ,не...
1
Периметр — это сумма длинн всех сторон.
Нужно найти длины векторов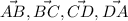 .
.
Длина вектора обозначается как
обозначается как 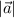 и вычисляется по формуле
и вычисляется по формуле
Координаты вектора AB находятся по формуле = {
= {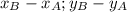 }, когда
}, когда  .
.
Вот и все формулы. Находим координаты четырёх векторов, находим длины этих векторов, складываем и находим тем самым периметр четырёхугольника ABCD.
Итак, A(-3; -2), B(2; 5), C(5; 2), D(0; -5).