1)найдите общий вид первообразных для функции: 2) вычислите интегралы 3) найдите площадь фигуры ограниченной линиями, , 4)вычислите: 5) решите уравнение:
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите письмо по английскому в формате ЕГЭ. Но не сложное, на...
3 - Сходства и различия народной сказки Снегурочка и пьесы Островского...
2 - Какие на ваш взгляд лучше достижения культуры были в 13-14 веках....
1 - Запишите однокоренные слова с приставками.гнать,держать, дышать,...
2 - Як засоби масової інформації впливають на рішення та поведінку...
3 - Корова привязана цепью длиной 9,7 м. Какая площадь доступна ей?...
3 - сделать все задания в Excel. Данные об оценках и тд брать из головы,...
2 - дайте ответы на во Рассказ Платонова Никита ...
2 - Задача 1Проведите анализ состава и структуры расходов торгового...
3 - Висота , проведена з вершини тупого кута ромба ділить сторону на...
2
1)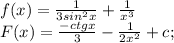
c є R
2)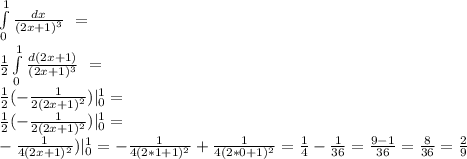
3) Ищем точки пересечения
точек пересечения нет, фигура неограничена, найти площадь не представляется возможным
4)![\sqrt[3] {-2\sqrt{2}}+\sqrt[6] {2}\sqrt [3]{2}=\\ \sqrt[3] {(-\sqrt{2})^3}+\sqrt[6] {2}\sqrt [6]{2^2}=\\ -\sqrt{2}+\sqrt[6] {2*2^2}=\\ -\sqrt{2}+\sqrt[6] {2^3}=\\ -\sqrt{2}+\sqrt {2}=0](/tpl/images/0106/8377/2ae85.png)
5)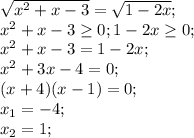
1-2*1<0 - корень 1 не подходит
-4 удовлетворяет
ответ: -4