1)найдите область определения функции: y=sinx+cosx 2) решите неравенство sin2xsinx-cos2xcos меньше или равно одной второй

Ответы

khavra1991 02.10.2020 16:57

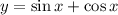
1) $y=\sin x +\cos x$

Область определения функции: множество всех действительных чисел, т.е.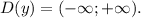 $D(y)=(-\infty;+\infty).$

2) $\sin2x\sin x-\cos 2x\cos x\leqslant \dfrac{1}{2}$

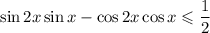
В левой части неравенства свернем под формулу косинуса суммы аргументов

$-(\cos 2x\cos x-\sin 2x\sin x)\leqslant \dfrac{1}{2}\\ \\ -\cos (2x+x)\leqslant \dfrac{1}{2}\\ \\ \cos 3x\geqslant -\dfrac{1}{2}$

Далее на окружности смотрим (на фото)...

$-\dfrac{2\pi}{3}+2\pi n\leqslant 3x\leqslant \dfrac{2\pi}{3}+2\pi n,n \in \mathbb{Z}\\ \\ \boxed{\boldsymbol{-\dfrac{2\pi}{9}+\dfrac{2\pi n}{3}\leqslant x\leqslant \dfrac{2\pi}{9}+\dfrac{2\pi n}{3},n \in \mathbb{Z}}}$

1)найдите область определения функции: y=sinx+cosx 2) решите неравенство sin2xsinx-cos2xcos меньше и

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

Stasya13203 03.03.2021 10:54

мне Произведение двух натуральных чисел, одно из которых на 6 больше другого равно 187. Найти эти числа....

dash4ka282863718 03.03.2021 10:54

Контрольна робота N4 Арифметична прогресія к 15:00 нужно здать...

nargiz999 30.05.2019 18:30

(2x-7)/(4-x) больше или равно 0 решить неравенство. желательно ход решения!...

vorobyv2004 30.05.2019 18:30

На завтра! тему не ! какое выражение должно быть записано в скобках: а) (степени)= 8 х 3 (степени) б) 2(степени)=81 а 2 (степени) в) (степени)= -27 у 3 (степени)...

alekcandrina200 30.05.2019 18:30

1.решите уравнение корень из 2 cos (п/4-x) - cosx =0.5. 2. зная. что sin t =3/5, 0...

polinakovaleva7 30.05.2019 18:30

70=100% х = 4%(пропорция) 100х=70*4 100х=280 х=280/100 х=2.8...

Sijjj777 30.05.2019 18:30

Решите систему уравнений: 1) x-y=6 x=6+y 2) x²+y²=20 (6+y)²+y²=20 36+12y+y²+y²-20=0 2y²+12y+16=0 y²+6y+8=0 d=9-8=1 x1=(-3+1)/1=-2 x2=(-3-1)/1=-4 как дальше...

anya64yankop08swl 30.05.2019 18:30

Надо! учитель ваще ! возведите в степень: а) (ху)4 (степени) б) (5n)2 (степени) в) (-10а)3 (степени) г) (3ах)3 (степени) д) (-сd)2 (степени) е) (-хуz)3 (степени)...

созданной 30.05.2019 18:30

Решите уравнение (3х-1)в квадрате - 9 х в квадрате = 10...

Legion2K17 16.03.2021 11:59

Напишите уравнение касательной ,проведенной к графику функции f(х)= -х^3+2х^2-5 в точке с абсциссой х_0=-3...

1)найдите область определения функции: y=sinx+cosx 2) решите неравенство sin2xsinx-cos2xcos меньше или равно одной второй

Популярные вопросы