1. Алгебра
  2. 1. Найдите координаты

1. Найдите координаты вершины параболы и нули функции: а) y=6 - х^2 б

ismailovu5 ismailovu5    2   17.03.2022 06:17    0

Ответы
iLFid iLFid  19.03.2022 12:50

а)координаты вершины параболы (0;6), нули функции: х₁=√6, х₂=-√6;

б) координаты вершины параболы (-10; 48), нули функции: х₁=-2, х₂=-8

Объяснение:

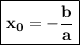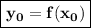для вычисления координат вершины параболы можно воспользоваться формулами \boxed{\displaystyle \bf x_0=-\frac{b}{a} } и \boxed{\displaystyle \bf y_0=f(x_0)}:

a)

\displaystyle y=6-x^2;\\x_0=-\frac{b}{a} =-\frac{0}{1} =0;\\y_0=f(x_0)=6-0^2=6-0=6\\ otvet:~~(0;6)

б)

\displaystyle y=3(x+5)^2-27;\\ y=3(x^2+10x+25)-27=3x^2+30x+75-27=3x^2+30x+48;\\x_0=-\frac{b}{a} =-\frac{30}{3} =-10;\\y_0=f(x_0)=f(-10)=3(-10+5)^2-27=3*(-5)^2-27=75-27=48;\\otvrt:~~(-10; 48)

чтобы найти нули функции, надо в уравнение графика подставить вместо у значение 0, иными словами, решить уравнение f(x)=0:

a)

y=6-x^2;\\ 6-x^2=0;\\x^2=6;\\x_{1,2}=\pm\sqrt{6}

б)

y=3(x+5)^2-27;\\y=3x^2+30x+48;\\3x^2+30x+48=0;\\x^2+10x+16=0;\\D=b^2-4ac=100-4*1*16=36;\\x_1=\frac{-b+\sqrt{D} }{2a} =\frac{-10+6}{2} =-2;\\x_2=\frac{-b-\sqrt{D} }{2a} =\frac{-10-6}{2} =-8

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Вениамин228 Вениамин228  27.01.2020 15:28
Разложите на множители 6xy(2x-y) + 5y (y-2x) ​...
Gromozeka1 Gromozeka1  27.01.2020 15:27
К[tex] \frac{3}{5} [/tex]числа 30 прибавьте [tex] \frac{2}{7} [/tex]числа 14​...
demyaniuk demyaniuk  27.01.2020 15:25
Решить логарфифмическое уравнение log3x+log3^1/2x+16=0...
lisyono525 lisyono525  27.01.2020 15:20
Найдите площадь , если я сделаю, то меня отпустят после 7 урока, а если не сделаю,то останусь на...
даша3648 даша3648  09.11.2020 11:05
Дано:ВО=ОЕ, АВС= Доказать:∆ BCO=∆ EFO Доказательство:Рассмотрим ∆ BCO и ∆ EFO ВО=ОЕ () ∠ВОС=∠ЕОF () ∠СВО и ∠АВС ,∠ОEF и∠DEF углы. По свойству смежных углов ∠АВС+ = и ∠DEF + = По условию...
barsik20002 barsik20002  09.11.2020 11:05
Дано зображення многогранників. На якому з малюнків прямі AB i CD не є мимибіжними? А. Б. В. Г....
serovik24 serovik24  09.11.2020 11:05
Помножить та звести подібні доданки . (m-4) (m+5)...
дима0951871812 дима0951871812  09.11.2020 11:05
Основание равнобедренной трапеции равны 14и34 её диаметр равен 100 найдите площадь трапеции...
lesikon11 lesikon11  09.11.2020 11:05
Постройте графики функций у=3^х и у=(1/3)^х на одной координатной плоскости. ​...
lthyperdeath1 lthyperdeath1  09.11.2020 11:05
Т 644оx — 8m2 — 8xРешение.325= 0;5 — 3х2х + 3Решение.2х2 - x+1162x = 4.x – 3Решение.​...

Популярные вопросы