1. Какова область определения функции y = fх? 2. Какова область значений функции у
√x?
3. Является ли функция у =
Nх возрастающей; убывающей;
монотонной; немонотонной?
4. Как по графику функции установить, является ли она выпу-
клой вверх? выпуклой вниз?
5. Как расположены друг относительно друга графики функций
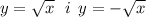
Другие вопросы по теме Алгебра
Популярные вопросы
- 1.какие тела называют наэлектризованными? 2.какие два рода электрических зарядов...
2 - Отношение падения реки к ее длине а )падение б)уклон...
1 - Как решить это уровнение 640: (25-x)=40...
2 - Эссэ на тему ,,интернет : друг или враг ?...
2 - Напишите сочинение на тему мой внутренний мир ....
2 - Напиши сочинение рассуждение на тему любимое телепередача...
3 - Напишите четырёхзначное число, которое делится на 9.может ли оно делится на 3?...
3 - Малға және тайғп сөзине сөйлем кұрап бериндерш...
1 - При каких значениях параметра a графики функций y=|x| и y = a+x^2: а) не имеют...
1 - :определи массу одного яблока на весах 5 яблок и 1 кг нарисованно. и ещё одна определи...
1
В данном случае, область определения функции y = f(x) не указана явно. Однако, по графику функции видно, что она определена только для неотрицательных значений x (x ≥ 0). Исходя из этого, можно сделать вывод, что область определения функции y = f(x) равна [0, +∞).
2. Область значений функции у = √x - это множество всех значений y, которые могут принимать функция при заданных значениях x.
Из графика функции y = √x видно, что она принимает все неотрицательные значения. То есть, область значений функции у = √x равна [0, +∞).
3. Чтобы определить, является ли функция у = Nx возрастающей, убывающей, монотонной или немонотонной, нужно анализировать ее поведение в зависимости от значения x.
Для функции у = Nx, где N - любое число, можно сделать следующие выводы:
- Если N > 0, то функция у = Nx будет возрастающей, так как с увеличением x значение y будет также увеличиваться.
- Если N < 0, то функция у = Nx будет убывающей, так как с увеличением x значение y будет уменьшаться.
- Если N = 0, то функция y = Nx будет принимать постоянное значение 0 и не будет возрастать или убывать.
- Если N не равно 0, то функция у = Nx будет немонотонной, так как ее поведение будет зависеть от значения N.
4. Чтобы определить, является ли функция выпуклой вверх или выпуклой вниз, нужно анализировать ее график.
Если график функции имеет форму "впуклой вниз" (как на графике y = -√x), то функция является выпуклой вниз.
Если график функции имеет форму "впуклой вверх" (как на графике y = √x), то функция является выпуклой вверх.
5. Исходя из графика функций y = √x и y = -√x, можно сделать следующие выводы:
- Оба графика представляют собой кривые, которые симметричны относительно оси y.
- График функции y = √x расположен выше оси x и принимает значения только в первом и втором квадрантах.
- График функции y = -√x расположен ниже оси x и принимает значения только в третьем и четвертом квадрантах.
Таким образом, графики функций y = √x и y = -√x пересекаются в точке (0, 0) и симметричны относительно оси y.