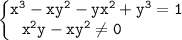1.из формулы s=at^2/2 выразите переменную t(все велечины положительны). 2. выражение 1дробь х-у * 1 дробь х=у * (х дробь у - у дробь х)
Другие вопросы по теме Алгебра
Популярные вопросы
- Бензальдегид+дихромат калия(K2Cr2O7)Бензальдегид+ H2???...
1 - Вопрос 1. Опишите разметку баскетбольной площадки. Перечислить!...
2 - Образ России в сказе Левша отношение к ней героев...
1 - Як змінювалося становище католицької церкви у XI -XV столітті?...
2 - А откуда взялась висота манометра???...
1 - Решите: какое логическое выражение соответствует следующей схеме?...
1 - Y=x³ обратная ей функция ...
1 - Improvizaţi dialoguri pe baza imaginilor din pag.136 на сегодня...
1 - Маша на 3 года старше Даши,а сумма их возрастов 27 лет.Сколько...
2 - У чому полягав вплив тогочасного СРСР на процеси, які в цей...
1
1.
ответ: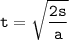
2.
ответ: