1. Алгебра
  2. 1)eсли разность корней уравнения

1)eсли разность корней уравнения 2,5х^2-10х+с=0 равна 2,5,то чему равно 2)найти корень уравнения: 2х^3+8х=х^2+4 3)сумма корней уравнения равна |х^2-2х-3|=3х-3

камил486 камил486    3   22.05.2019 12:50    1

Ответы
vanessashevchuk vanessashevchuk  17.06.2020 23:26

1) Согласно всяких терем Виетта или обратных им или следствий из них - уже не помню:

x_1+x_2=-\frac{b}{a} = x_1+x_2=-\frac{-10}{2.5}=4 \\\ x_1x_2=\frac{c}{a} = x_1x_2=\frac{c}{2.5} = c=2.5x_1x_2

Имеем систему уравнений

\left \{ {{x_1+x_2=4} \atop {x_1-x_2=2.5}} \right. \\\ \left \{ {{2x_1=6.5} \atop {x_1-x_2=2.5}} \right. \\\ \left \{ {{x_1=3.25} \atop {x_2=0.75}} \right. \\\ = c=2.5*3.25*0.75=6,09375

 

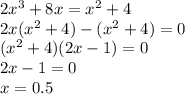
2) 2x^3+8x=x^2+4 \\\ 2x(x^2+4)-(x^2+4)=0 \\\ (x^2+4)(2x-1)=0 \\\ 2x-1=0 \\\ x=0.5

 

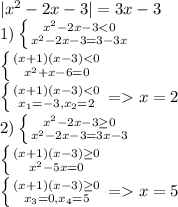
3) |x^2-2x-3|=3x-3 \\\ 1) \left \{ {{x^2-2x-3<0} \atop {x^2-2x-3=3-3x}} \right. \\\ \left \{ {{(x+1)(x-3)<0} \atop {x^2+x-6=0}} \right. \\\ \left \{ {{(x+1)(x-3)<0} \atop {x_1=-3, x_2=2}} \right. = x=2 \\\ 2) \left \{ {{x^2-2x-3 \geq0} \atop {x^2-2x-3=3x-3}} \right. \\\ \left \{ {{(x+1)(x-3) \geq0} \atop {x^2-5x=0}} \right. \\\ \left \{ {{(x+1)(x-3) \geq0} \atop {x_3=0, x_4=5}} \right. = x=5

Сумма корней 2+5=7.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
NJR228337 NJR228337  06.07.2019 11:40
Брат на 2 года младше сестры. сколько лет брату и сколько сестре, если вместе им 20 лет...
Mia112 Mia112  06.07.2019 11:40
Используя свойство дроби найдите значение a при котором a/8=14/15...
vikarubachok vikarubachok  06.07.2019 11:40
Исследуйте функцию y=3|x| - x квадрат на четность...
gnatiuk1981 gnatiuk1981  29.08.2019 20:20
2x-y=4 y=6 построить график линейного уравнения....
searchsignal searchsignal  29.08.2019 20:20
При каком значении a система уравнений(сама система): 2х+3у=5 ах-6у=-10 имеет бесконечно много решений?...
Кролик1922 Кролик1922  29.08.2019 20:20
Найдите наименьшее целое решение неравенств 1/х-2+1/х-1 =1/х...
anisimowaanastowf62v anisimowaanastowf62v  29.08.2019 20:20
Даны две временные величины х и у, находящиеся в пропорциональной зависимости. известно, что х=2 у=6. выразите формулой зависимость у от х....
andrekonushew andrekonushew  29.08.2019 20:20
Выполнить действия : а) (4а²+b²)(2a-b)(2а+b); б) (b²c³-2a²)(b²c³+2a²)....
Кисулятв Кисулятв  29.08.2019 20:20
(x+1)(2x-8)(3x+6) 0 неравенство...
паша5808989 паша5808989  29.08.2019 20:20
Найдите точки экстремума функции 1)y=1/3x^3-2.5x^2+6x-9 2)докажите что функция y=5/3-x в области определения возрастант если можно на листочке...

Популярные вопросы