.(1)цену на книгу снизили на 10%, в результате чего она стоит теперь 45,9 рублей. сколько стоила книга до снижения цены? . 2)расстояние между пристанями катер проходит по течению реки за 2 часа, а против течения за 3 часа. какова
скорость катера в стоячей воде, если скорость течения реки 5 км/ч? скорость катера обозначить за х км/ч 3)решите неравенство 3х+1≥2(х-1)+6х 4)найдите сумму корней уравнения 16х²-4=0).
Другие вопросы по теме Алгебра
Популярные вопросы
- Какой самый известный царь в месопотамии?...
3 - 7. переведите на язык. 4 магазина, 7 долларов, 13 заводов, 19 фабрик, 42 года,...
2 - 6. заполните пропуски предлогами и переведите предложения на язык. come the room,...
2 - Замените разговорное слово « выпалил» из ниже фрагмента стилистически нейтральным...
1 - 4. образуйте сравнительную и превосходную степени прилагательных. interesting,...
2 - Назовите основные части двигателя внутреннего сгорания и их назначения....
1 - Язык 6 класс урок 8 7 выполните по образцу танцевать, рисовать,плавать,читать образец:...
1 - Найдите наибольшее целое значения x, удовлетворяющее неравенству arctgx 0...
3 - Откуда происходит название двигателя внутреннего сгорания?...
2 - Выберите существительное в общем или притяжательном падеже в зависимости от смысла....
1
№ 1
х рублей стоила книга до понижения цены
0,1х рублей - 10% скидка на книгу
х - 0,1х = 45,9
0,9х = 45,9
х = 45,9 : 0,9
х = 51
ответ. 51 рубль стоила книга до понижения цены
№ 2
х км/ч собственная скорость катера,
(х+5) км/ч скорость катера по течение
(х-5) км/ч скорость катера против течения
2(х+5) = 3(х-5)
2х + 10 = 3х - 15
3х - 2х = 10 + 15
х = 15
ответ. 15 км/ч собственная скорость катера.
№ 3
3х+1≥2(х-1)+6х
3х+1≥2х-2+6х
2+1≥ 8х - 3х
3 ≥ 5х
х ≤ 0,6
ответ. x∈( - ∞, 0,6]
№ 4
16х²-4=0
16х²= 4
х²= 4/16
х²=1/4
х1 = -1/2
х2 = 1/2
х1 + х2 = -1/2 + 1/2 = 0
ответ. х1 + х2 = 0.
1) Пусть x рублей - начальная цена книги, тогда на 0,1x рублей подешевела книга. Известно, что теперь она стоит 45,9 рублей.
Составляем уравнение:
x-0,1x=45,9
0,9x=45,9
x=51
ответ: 51 рубль.
2) Пусть x км/ч - собственная скорость катера, тогда (x+5) км/ч - скорость катера по течению, (х-5) км/ч - скорость катера против течения. Известно, что расстояние между пристанями катер проходит по течению реки за 2 часа, против течения - за 3 часа. Расстояние между пристанями равно 2(х+5) км или 3(х-5) км.
Составляем уравнение:
2(х+5)=3(х-5)
2х+10=3х-15
2х-3х=-15-10
-х=-25
х=25
ответ: 25 км/ч.
3)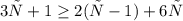
(-![(-\infty; 0,6]](/tpl/images/0028/3562/4534f.png)
4)