1. а) при каком условии неполное квадратное уравнение имеет корни, равные по но противоположные по знаку? модулю, b) напишите общий вид неполного квадратного уравнения, которое имеет единственный корень.

Общий вид квадратного уравнение следующее

a·x²+b·x+c=0, где a≠0.

Неполное квадратное уравнение имеет один из следующих видов:

1. a) Если неполное квадратное уравнение имеет вид a·x²+c=0 и c/a<0, то квадратное уравнение a·x²+c=0 имеет корни равные по модулю, но противоположные по знаку:

a·x²+c=0  ⇔   a·x² = -c  ⇔  x² = -c/a, так как -c/a>0  ⇔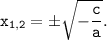

Тогда

Отсюда условие:

b=0 и c/a<0!

b) Если неполное квадратное уравнение имеет вид a·x²=0, то квадратное уравнение a·x²=0 имеет единственный корень:

a·x²=0  ⇔  x²=0  ⇔ x=0.

Отсюда условие:

b=c=0!

В случае a·x²+b·x=0 квадратное уравнение имеет два корня:

a·x²+b·x=0  ⇔ x·(a·x+b)=0 ⇒ x₁=0, x₂= -b/a.

Объяснение:

1) а) корни равны по величине, но противоположны по знаку.

a(x-x0)(x+x0) = 0

ax^2 - a*x0^2 = 0

б) корни равны по величине, но противоположны по модулю.

Таких не бывает, потому что модуль всегда не отрицателен.

Модули не могут быть противоположны друг другу.

2) неполное квадратное уравнение, которое имеет единственный корень:

ax^2 = 0

x1 = x2 = 0