1, 27, 729,
ответы: 3¹⁷, 3¹⁹, 3²², 3³⁰,3⁴¹
Другие вопросы по теме Алгебра
Популярные вопросы
- Во по новелле П. Мериме «Маттео Фальконе» ответе Расскажите...
1 - Спустя сколько лет после утраты государственной независимости...
2 - Знайти область визначення функції y=√x(x - 4)...
2 - Пример 1Среди данных уравнений с двумя переменными выберите...
3 - Написать в ми бемоль мажор: обращение T53, S53, D53, D7....
2 - Вычисли, сколько энергии поступает на 2-й трофический уровень...
2 - Плюсы и минусы Интернета480. Литературный диктант.1. В этой...
3 - Найти точки максимума, минимума, промежутки возрастания и убывания...
1 - Разложи на множители: 6x²+12xy+6y² Известно, что один множитель...
3 - Бактериялардың шаруашылықтағы маңызы эссе...
1
Один из показателей степени числа 3 может быть представлен в виде . Поэтому одно из представленных чисел может быть членом данной геометрической прогрессии - это число
. Поэтому одно из представленных чисел может быть членом данной геометрической прогрессии - это число 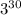 .
.
Можно представить заданную прогрессию таким образом :