1.2. (aₙ) — арифметическая прогрессия; a₁ = 5; a₂ = 3. Найдите a₁₈. Варианты ответа: А) -31; Б) -27; В) -25; Г) -28; Д) -29. 1.4. Найдите сумму всех натуральных чисел, которые кратные 3 и не больше чем 150.
1.5. Какое из приведённых чисел является членом геометрической прогрессии 1; 4; 16; ...? А) 2; Б) 2¹⁵; В) 2¹⁹; Г) 2¹²⁰; Д) 2¹⁷⁵
1.6. Найдите сумму первых восьми членов геометрической прогрессии -1; 2; -4; ... .

Ответы

unitolog 14.05.2021 19:26

$1.2)\ \ \{a_{n}\}:\ \ 5\ ;\ 3\ ;\ ...\\\\a_1=5\ ,\ a_2=3\\\\d=a_2-a_1=3-5=-2\\\\a_{18}=a_1+17d=5+17\cdot (-2)=5-34=\boxed{-29}$

$1.4)\ \ \{a_{n}\}:\ \ 3\ ;\ 6\ ;\ 9\ ;\ 12\ ;\ 15\ ;\ 18\ ;\ ...\ \ \ \ \ ,\ \ \ a_{n}\leq 150\\\\d=a_2-a_1=3\ \ ,\ \ a_{n}=a_1+d(n-1)=3+3(n-1)=3n\\\\3n=150\ ,\ \ n=50\\\\S_{50}=\dfrac{a_1+a_{50}}{2}\cdot 50=\dfrac{3+150}{2}\cdot 50=153\cdot 25=\boxed{3835}$

$1.5)\ \ \{b_{n}\}:\ \ 1\ ;\ 4\ ;\ 16\ ;\ ...\\\\q=\dfrac{b_2}{b_1}=\dfrac{4}{1}=4\ \ ,\ \ \ \ b_{n}=b_1q^{n-1}=4^{n-1}\\\\a)\ \ 4^{n-1}\ne 2\ \ ,\ \ esli\ \ n\in N\\\\b)\ \ (4)^{n-1}=2^{15}\ \ ,\ \ 2^{2n-2}=2^{15}\ \ \to \ \ 2n-2=15\ ,\ \ 2n=17\ \ ,\\\\n=8,5\notin N\\\\c)\ \ 4^{n-1}=2^{19}\ \ ,\ \ 2^{2n-2}=2^{19}\ \ ,\ \ 2n-2=19\ ,\ \ 2n=21\ \ ,\ \ n=10,5\notin N$

$d)\ \ 4^{n-1}=2^{120}\ \ ,\ \ 4^{n-1}=4^{60}\ \ ,\ \ n-1=60\ \ ,\ \ \underline{n=61\in N}\\\\e)\ \ 4^{n-1}=2^{175}\ ,\ \ 2^{2n-2}=2^{175}\ \ ,\ \ 2n-2=175\ \ ,\ \ 2n=177\ \ ,\ \ n=88,5\notin N$

ответ: членом заданной геометр. прогрессии является число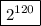 $\boxed{2^{120}}$ .

$1.6)\ \ \{b_{n}\}:\ \ -1\ ;\ 2\ ;\ -4\ ;\ ...\\\\b_1=-1\ \ ,\ \ b_2=2\ \ \to \ \ \ q=\dfrac{b_2}{b_1}=\dfrac{2}{-1} =-2\\\\S_8=\dfrac{b_1\, (q^8-1)}{q-1}=\dfrac{-1\cdot ((-2)^8-1)}{-2-1}=\dfrac{256-1}{3}=\dfrac{255}{3}=\boxed{85}$